Автоколебания напорных систем и разрушение гидроагрегатов

Роль математической физики – это правильно ставить вопросы; решить их может только опыт.
А. Пуанкаре

Краткое содержание

В работе рассмотрено возбуждение гидроакустических автоколебаний в напорных водоводах гидроэлектростанций с высокими плотинами. Если этот процесс развивается при расходах воды б?льших, чем ее расход на рабочем режиме, то происходит практически неограниченный рост пульсаций давления в водоводе. Именно автоколебания явились причиной катастрофы на Саяно-Шушенской ГЭС 17 августа 2009 года, а также аварии на Нурекской ГЭС 9 июля 1983 года.

На основе решений волнового уравнения с разрывным граничным условием, моделирующим турбину, сравнения полученных в этих решениях собственных частот с частотами возбуждения и учета коэффициентов затухания выведен критерий возбуждения автоколебаний для определения гидроакустической устойчивости ГЭС. Вычислены индексы гидроакустической устойчивости девяти гидроэлектростанций различных типов. К списку из двух гидроэлектростанций, продемонстрировавших гидроакустическую неустойчивость на практике, добавлены ГЭС на границе устойчивости и неустойчивый расчетный вариант еще одной гидроэлектростанции. Приведены списки всех существующих и строящихся ГЭС большой и средней мощности с высотой плотины больше 200 м, являющихся потенциально наиболее опасными с рассматриваемой точки зрения.

I – Основные принципы

Как известно, 17 августа 2009 года в 8 часов 13 минут по местному времени на Саяно-Шушенской гидроэлектростанции им. П. С. Непорожнего из турбинного колодца на высоту около 14 м был выброшен второй гидроагрегат, который незадолго до этого персонал станции попытался остановить. Во время инцидента произошло полное разрушение гидроагрегата. Его авария привела к катастрофическому развитию событий на станции. Вода, под большим давлением хлынувшая из открытого турбинного колодца, разрушила часть конструкций машинного зала и уничтожила важнейшие подсистемы других агрегатов, что привело к выходу их из строя и частичному или полному разрушению. Машинный зал и помещения под ним были затоплены. К 9 часам 20 минутам с гребня плотины вручную были закрыты аварийно-ремонтные затворы на водоводах всех гидроагрегатов и, таким образом, был прекращен доступ воды с верхнего бьефа в машинный зал [1, 2]. За 26 лет до этого, 9 июля 1983 года в 22 часа 48 минут, через 4 минуты после включения в сеть первого гидроагрегата, на Нурекской ГЭС также произошел частичный отрыв его крышки [3]. Объяснить причину этого инцидента тогда не удалось.

В работах [2, 3] было показано, что оба инцидента произошли в результате неконтролируемого роста пульсаций давления в напорных водоводах гидроагрегатов. Единственная известная непротиворечивая теория, объясняющая это явление, как с качественной, так и с количественной точек зрения, – это теория резонансного возбуждения автоколебаний напорных систем [3, 4], являющаяся развитием теории гидроакустического резонанса [5 – 7]. Опишем здесь вкратце основные положения этой теории, и несколько более подробно остановимся на тех практических выводах из нее, которые стоило бы принять во внимание гидроэнергетикам, проектирующим, строящим и эксплуатирующим высоконапорные гидроэлектростанции.

Из теории следует, что для того, чтобы пульсации давления в водоводе возрастали по времени, необходимо выполнение двух условий:

1. На стационарной характеристике турбины (зависимости относительных потерь полного давления ?p/p от безразмерного расхода q = Q/Q^*, Q^*– объемный расход воды на рабочем режиме) должен существовать падающий участок, где производная полного давления по расходу отрицательна (см. рисунок).

2. Частота прецессии вихря за турбиной или других достаточно мощных источников колебаний давления, например, частота вращения ротора турбины, и собственная частота колебаний воды в водоводе должны быть близки между собой.

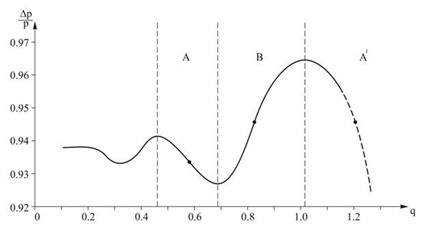
На рисунке, построенном на основе экспериментальных данных, полученных при натурных испытаниях десятого гидроагрегата Саяно-Шушенской ГЭС [5], вертикальными пунктирными линиями выделены зоны, в которых производная функции ?p/p (за исключением их границ) сохраняет постоянный знак. Именно зоны A и A’ являются теми областями, где возможно возникновение разрушительных автоколебаний в водоводе ГЭС (следует отметить, что в зоне B возможно возникновение автоколебаний в водоводе гидроаккумулирующей станции при работе ее агрегата в насосном режиме [4]). При указанных выше условиях под действием внешнего периодического возмущения может произойти возбуждение автоколебаний из-за наличия в колебательном контуре нелинейного элемента, создающего положительную обратную связь. Роль такого элемента играет турбина на падающих участках своей стационарной характеристики.

Второе необходимое условие с достаточной для возбуждения автоколебаний точностью реализуется, к счастью, сравнительно редко. Частота прецессии вихря за турбиной (вихревая частота) ?_v зависит от частоты вращения ротора турбины ?_r и степени отставания от ротора несимметричного вращающего отрыва, которая определяется особенностями обтекания турбины. Частота собственных колебаний воды в водоводе ?_e зависит от его геометрии и с частотой вращения турбины прямо не связана.

Поэтому, для предварительного решения поставленной задачи следует найти гидроэлектростанции, у которых

где частота возбуждения ?_p = ?_v или ?_p = ?_r, причем, как показали дальнейшие расчеты, в большинстве случаев, в том числе и в обоих инцидентах, произошедших в реальности, опасной оказывается близость частот собственной ?_e и вихревой ?_v.

II – Элементы теории резонансного возбуждения автоколебаний напорных систем

На основе теории размерностей [8], было показано [3], что вихревая частота ?_v в первом приближении пропорциональна частоте вращения ротора турбины ?_r:

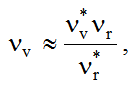    (1)

где индекс ^* относится к известным из эксперимента характерным значениям этих параметров. Выражение (1) позволяет пересчитывать вихревые частоты различных гидроагрегатов в том случае, когда параметры оптимальности сравниваемых радиально-осевых турбин ? не слишком сильно различаются между собой (для высоконапорных ГЭС ? ? 30 – 50, для средненапорных – ? ? 50 – 70 [3]). Поэтому, в качестве характерных частот при пересчете в первом случае используются соответствующие частоты агрегатов Саяно-Шушенской ГЭС, а во втором – Красноярской ГЭС [3, 9]. Данный комплексный эмпирический параметр вычисляется следующим образом:

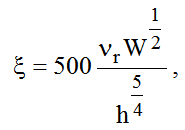
где частота ?_r измеряется в герцах, мощность W в мегаваттах, напор h в метрах.

Собственная частота колебаний в водоводе ?_e определяется посредством решения методом Фурье одномерного волнового уравнения с сильным разрывом – перепадом полного давления на турбине [3]. Именно этот разрыв давления, соизмеримый по величине с изменением давления во всем водоводе превращает хорошо известную линейную задачу малых колебаний жидкости в трубе с открытыми концами [10, 11] в нелинейную [5, 6]. Был построен регулярный метод расчета нелинейной системы уравнений гидроакустических колебаний и после массовых расчетов были выявлены качественные свойства решений этой системы уравнений в области практически интересных значений определяющих параметров. Анализ свойств решений системы уравнений в этой области позволил найти простой метод оценки собственных частот типичных водоводов, который может быть использован любым инженером [3].

Как показали дальнейшие исследования, для более точной оценки устойчивости напорных систем необходимо достаточно точно знать коэффициент затухания колебаний ? в точках максимумов стационарной характеристики турбины. Для Саяно-Шушенской ГЭС этот параметр был определен из сопоставления расчетных и экспериментальных данных. Анализ основных факторов, вызывающих затухание колебаний (диссипации энергии колебаний в водоводе и излучения энергии через его открытые концы) позволил построить метод пересчета этого параметра для других гидроэлектростанций [3].

III – Вычисление индекса устойчивости

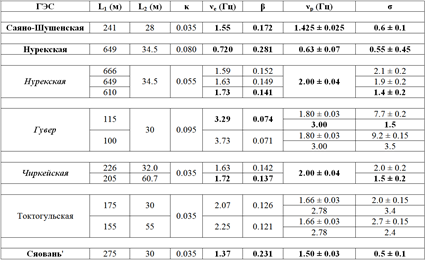
Результаты применения разработанной полуэмпирической теории к группе средне- и высоконапорных гидроэлектростанций в самом простом инженерном варианте представлены в таблице 1.

Таблица 1

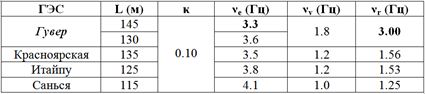
Здесь L – полная длина водовода (сумма длин его напорной части и отсасывающей трубы), ? = 1 – ?p/p в соответствующих точках максимума стационарной характеристики турбины. Сравнивая частоты собственных колебаний водоводов ?_e и вихревые частоты ?_v, а также турбинные частоты ?_r у четырех рассматриваемых гидроэлектростанций, можно наглядно убедиться, что вследствие большого различия частот у трех средненапорных ГЭС (Красноярской, Итайпу и Санься (Три Ущелья)) нет опасности возникновения автоколебаний.

У высоконапорной гидростанции Гувер собственные частоты более длинного водовода оказались в опасной близости к турбинным частотам. Отношение | ?? |/?_e < 0.1 примерно такое же, как у Саяно-Шушенской и Нурекской ГЭС [3]. Поэтому эту гидроэлектростанцию следует отнести к группе риска и оценить ее гидроакустическую устойчивость более точным методом.

Для этого при использовании результатов классической теории резонансного возбуждения колебательной системы с затуханием [12] была получена оценка условий жесткого возбуждения автоколебаний в напорной системе гидроэлектростанции:

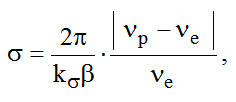
где

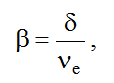
? – индекс устойчивости гидроакустической системы, характеризующий степень резонансного отклика колебательной системы, состоящей из напорного водовода, турбины и отсасывающей трубы, на внешнее колебательное возмущение, k_? – нормирующий множитель, величина которого по результатам расчетных и экспериментальных данных для Саяно-Шушенской ГЭС была принята равной 5, ? – коэффициент затухания в точке максимума стационарной характеристики турбины [3]. Смысл введения нормирующего множителя состоит в том, чтобы описанная ниже критическая величина индекса устойчивости ?^* не слишком отличалось от 1, а также практически не зависела от точности определения коэффициента затухания ? [13].

Результаты расчетов возбуждения автоколебательных процессов для шести высоконапорных ГЭС представлены в таблице 2. Во всех случаях, кроме первого из представленных вариантов для Нурекской ГЭС (для него был проведен расчет в зоне A) рассматривался режим возбуждения автоколебаний в зоне A’, который приводит к катастрофическому сценарию дальнейшего развития событий. Для Нурекской ГЭС из-за большой длины ее водоводов режимы были рассчитаны на второй моде колебаний (рассмотрены самый длинный (третий) и самый короткий (восьмой) водоводы, а также водовод первого гидроагрегата, на котором ранее произошла авария 9 июля 1983 года, когда его турбинная крышка была частично оторвана) [3]. Для ГЭС Гувер и Токтогульской представлены значения индекса ? для частот возбуждения как вихревой, так и турбинной, а для остальных – только для вихревой частоты, так как турбинные частоты там гораздо удаленнее от частот собственных колебаний водовода и никакой опасности собой не представляют.

Уровень колебательного возмущения, при котором система в процессе жесткого возбуждения переходит в автоколебательный режим, может быть приблизительно оценен из имеющихся натурных данных: по крайней мере, в двух случаях этот режим был запущен, во многих других – нет [3]. Кроме того, известно, что на двух гидроаккумулирующих станциях Далечице и Жарновец происходило приближение к режиму возбуждения автоколебаний [4]. Для всех этих случаев можно подсчитать индекс устойчивости, и граница раздела между ними даст критический уровень индекса ?^*. Рассмотрим имеющиеся экспериментальные данные.

Таблица 2

Прямым жирным шрифтом в таблице 2 выделены неустойчивые гидроэлектростанции, а косым жирным шрифтом – ГЭС, приближающиеся к границе устойчивости и, видимо, могущие ее перейти при очень сильных возмущениях, вносимых в работу их гидроагрегатов. Первые 2 строки таблицы 2 относятся к случаям инцидентов на Саяно-Шушенской и Нурекской ГЭС. На последней станции авария произошла в зоне A на первой моде колебаний. Все остальные представленные в таблице 2 расчеты проведены для зоны A’, при этом для Нурекской ГЭС в строках 3 – 5 показаны результаты расчетов уже на второй моде колебаний, так как на первой моде в зоне A’ у нее никаких проблем с гидроакустической устойчивостью заведомо не существует. Именно поэтому собственная частота водовода первого агрегата станции на этом режиме возросла примерно в два с четвертью раза [3].

Вариант Сяовань’ – чисто расчетный. Так как длины водоводов этой строящейся китайской гидроэлектростанции неизвестны, они, в предположении конструктивного подобия ее плотины были пересчитаны с длин водоводов Саяно-Шушенской и Чиркейской ГЭС. В реальности как конструкция и длина водоводов ГЭС Сяовань, так и индекс ее гидроакустической устойчивости, вполне могут быть иными.

Из таблицы 2 следует, что в тех случаях, когда происходили отрывы турбинной крышки (на Саяно-Шушенской и Нурекской ГЭС), индекс гидроакустической устойчивости ? оказывался меньше 1. При ? ? 1.1 – 1.2 начинались недопустимые вибрации гидроагрегатов на ГАЭС Далечице и Жарновец [4]. Когда , серьезных гидроакустических проблем, видимо, не наблюдалось. Следовательно, по имеющимся данным условием возбуждения автоколебаний оказывается следующее:

где ?^* – критическое значение индекса устойчивости.

Согласование между результатами теории резонансного возбуждения автоколебаний и экспериментальными данными, полученными при эксплуатации 11 ГЭС и ГАЭС, рассмотренными в [3, 4], а также Ингури ГЭС, доказывает, что эта теория достаточно адекватно отражает реальные процессы, происходящие в напорных системах гидроэлектростанций при потере ими гидроакустической устойчивости, и что ее можно использовать для поиска неустойчивых гидроэлектростанций. Таким образом, если индекс гидроакустической устойчивости ? < 1, то гидроагрегат может вылететь из своего турбинного колодца.

IV – Список существующих ГЭС, входящих в зону гидроакустического риска

В предыдущих разделах было показано, что для возбуждения автоколебаний в напорной системе необходима близость частоты внешнего периодического возмущения, которое возникает из-за вращения ротора гидроагрегата или из-за прецессии затурбинного вихря, и частоты собственных колебаний воды в водоводе. Частота вращения ротора коррелирует с напором воды на номинальном рабочем режиме агрегата – чем выше напор, тем, как правило, больше эта частота. Частота прецессии затурбинного вихря (вихревая частота) в свою очередь зависит от частоты вращения ротора, тогда как собственная частота колебаний в основном определяется длиной водовода. В случае, когда водоводы расположены как на Саяно-Шушенской ГЭС на фронтальной поверхности плотины, их собственные частоты также коррелируют с напором, но противоположным образом – чем выше напор, тем длиннее водоводы, и тем ниже частоты собственных колебаний напорной системы.

Отсюда следует, что существует некий диапазон напоров, а, значит, и высот плотин, в котором возможен этот опасный процесс – возбуждение автоколебаний. Данный диапазон напоров можно назвать зоной гидроакустического риска. В том случае, когда водоводы расположены вне плотины, например, пробиты в окружающих станцию скалах, как на Нурекской ГЭС, а также, когда существенный вклад в напор вносит деривация, как на Ингури ГЭС и большинстве высокогорных альпийских станций, априорную оценку возможной принадлежности станции к зоне риска сделать сложнее. Однако, как показывает даже самое первичное знакомство с плотинно-деривационными гидроэлектростанциями, они характеризуются, как правило, очень длинными туннелями, подводящими воду, и отходящими от них очень короткими напорными водоводами. Так что при предварительном обзоре гидроэлектростанций, вероятно находящихся в зоне гидроакустического риска, такие ГЭС, за исключением отдельных случаев, можно не рассматривать. В то же время, как показано выше, в зоне риска вполне могут оказаться станции типа Нурекской ГЭС. Поэтому, при отсутствии информации о том, какими на самом деле являются водоводы на многих плотинных гидроэлектростанциях, при самом первом рассмотрении можно считать потенциально опасными все станции с соответствующей высотой плотин вне зависимости от конструкции их водоводов.

Целесообразно сосредоточиться на ГЭС, которые входят в группу риска с достаточно высокой степенью вероятности, не распыляя внимания на те станции, опасность для которых минимальна. Вследствие этого в двух последних разделах статьи рассматриваются только ГЭС с высотой плотины не ниже 200 м. Исключаются из списка, как уже указывалось ранее, плотинно-деривационные гидроэлектростанции с короткими водоводами. Не рассматриваются также гидроаккумулирующие станции, которых в мире сейчас насчитывается около 300 [14], несмотря на то, что, по крайней мере, на двух из них зарегистрированы явления, которые были интерпретированы как приближение к опасному гидроакустическому режиму [4]. Это связано с тем, что длины водоводов ГАЭС не коррелируют с их напорами, и для оценки гидроакустического риска необходимы точные данные о конструкции этих станций. Поэтому для них не представляется возможным провести такой предварительный обзор, хотя совершенно не исключено, что какие-то из них также могут входить в группу риска.

В соответствии с заявленными принципами был составлен, видимо, практически полный мировой список ГЭС с высотой плотины не ниже 200 м, и с мощностью хотя бы одного из радиально-осевых агрегатов станции не меньше 100 МВт. При меньших мощностях нет гарантии достаточной точности применяемой в работе [3] теории подобия, да и инциденты на маломощных станциях не столь опасны. Все источники информации, использованные при составлении этого списка, указывать вряд ли целесообразно вследствие их многочисленности, поэтому представлена только исходная ссылка на неполный список самых высоких плотин мира [15].

Таблица 3

Итак, всего в мире насчитывается 24 гидроэлектростанций большой и средней мощности, по предварительным данным входящих в группу риска по гидроакустической устойчивости. Общая их мощность составляет около 37.5 ГВт, и все вместе они по мощности примерно эквивалентны 6 Саяно-Шушенским ГЭС. Из этих 24 станций характеристики гидроакустической устойчивости выше подробно рассматривались у 5, в таблице 3 их названия выделены косым шрифтом. Только у двух из них (выделены жирным шрифтом) индекс гидроакустической устойчивости ? оказался меньше 1, и именно там произошли два известных инцидента с отрывами турбинной крышки [3]. Многие станции из этого списка работают достаточно давно, и, скорее всего, гидроакустические характеристики большинства из них приемлемы для безопасной эксплуатации. Однако, все же было бы чрезвычайно полезно рассчитать и их индексы устойчивости. Но для этого необходимо знать набор их параметров, указанный в инструкции [16], чего невозможно достичь без прямых контактов с эксплуатантами этих станций. Вследствие отсутствия этих данных можно сделать только самую грубую оценку вероятности того, что высоконапорная гидроэлектростанция может быть гидроакустически неустойчива, деля число ГЭС, на которых произошли подобные инциденты, на общее число станций. Эта вероятность оказывается близка к величине 0.1.

Следует упомянуть также о не входящей в данный список гидроэлектростанции Памир-1 (Таджикистан), мощность которой заметно меньше, чем у любой из станций, рассматриваемых в этой статье, и, поэтому, ее характеристики, как будто бы, выходят за пределы возможной области пересчета параметров по подобию. Тем не менее, эта ГЭС интересна тем, что 5 февраля 2007 года на ней также произошла авария с отрывом турбинной крышки второго гидроагрегата и ее вылетом (очевидно, вместе с ротором агрегата) из турбинного колодца. Машинный зал был полностью затоплен, однако человеческих жертв там не было. В качестве причины случившегося назывался гидравлический удар, однако почему он возник, разъяснений не последовало [17]. Интересно отметить, что инцидент произошел при «сокращенном» расходе воды вследствие замерзания водохранилища. Другой, более поздний вариант объяснения выброса агрегата – «из-за повышения уровня воды в ирригационном канале» [18]. Таким образом, официальные объяснения, как минимум, противоречивы, а вся картина объективно очень похожа на то, что произошло в двух инцидентах с возникновением автоколебаний в напорных водоводах на Саяно-Шушенской и Нурекской ГЭС. Однако, заключение о возможности возбуждения автоколебаний в напорной системе ГЭС Памир-1 пока дано быть не может, так как неизвестен полный набор ее технических характеристик, необходимых для расчета индекса ее гидроакустической устойчивости.

V – Список строящихся ГЭС, входящих в зону гидроакустического риска

Первое десятилетие XXI века характеризуется невиданным ранее ростом интенсивности строительства гидроэлектростанций, относимых к группе риска, притом, что незадолго до начала ввода в строй первых из этих станций произошла катастрофа на Саяно-Шушенской ГЭС, которую следует рассматривать как грозное предупреждение о возможном будущем некоторых станций из этого списка (см. таблицу 4). Общая мощность таких гидроэлектростанций составляет около 130 ГВт, что примерно равно мощности 20 Саяно-Шушенских ГЭС, и планируется, что все они должны войти в строй во втором десятилетии XXI века.

Таблица 4

Гидроэлектростанция Лонгтан (Longtan) уже начинает работать (двадцать шестой номер в таблице 4). Первый агрегат очередной китайской ГЭС – Сяовань (Xiaowan) (восьмой номер в таблице 4) должен быть запущен в конце этого 2010 года. Некоторые из станций данного списка, например, Рогунская, Siang Upper или Худони в реальности, быть может, не будут построены так быстро, как планируется сейчас. Однако есть мало сомнений в том, что конвейер по постройке 17 китайских гидроэлектростанций с высотой плотины более 200 м и общей мощностью примерно эквивалентных 14 Саяно-Шушенским ГЭС, не собьется с графика, если его организаторы не столкнутся с неожиданными для них явлениями, подобными тем, что произошли на Саяно-Шушенской ГЭС 17 августа 2009 года. А возможность этого, как представляется из сопоставления таблиц 3 и 4, существует – вполне можно ожидать, что 2 – 3 стации из таблицы 4 и из них 1 – 2 китайские могут оказаться гидроакустически неустойчивыми, и тогда рано или поздно их будет ждать судьба Саяно-Шушенской ГЭС. Общие потери от катастрофы в Саянах оцениваются в 3 миллиарда долларов, так что возможные потери от таких инцидентов могут быть порядка нескольких миллиардов долларов, не говоря уже о возможных человеческих жертвах. Более точное представление о будущих рисках гидроэлектростанций из таблицы 4 можно получить после расчета их индексов гидроакустической устойчивости. Необходимая для этого информация может быть предоставлена, по-видимому, только компаниями, занятыми их постройкой, причем именно эти компании более чем кто-либо и должны быть заинтересованы в том, чтобы эти расчеты были сделаны.

Выводы

1. Построена теория резонансного возбуждения автоколебаний напорных систем, позволяющая оценить гидроакустическую устойчивость гидроэлектростанций, потеря которой привела к катастрофе на Саяно-Шушенской ГЭС.

2. Вычислены индексы гидроакустической устойчивости девяти ГЭС и ГАЭС, причем только на тех станциях, где происходили инциденты с необъяснимыми отрывами турбинных крышек, этот индекс оказался меньше 1.

3. Составлены мировые списки потенциально наиболее опасных с гидроакустической точки зрения существующих и строящихся гидроэлектростанций.

Ссылки

1. Ю. И. Лобановский – Иерихон на Енисее. ТехНАДЗОР, N 11 (36), ноябрь 2009

2. Ю. И. Лобановский – Технические причины катастрофы на Саяно-Шушенской ГЭС (итоги расследования), ноябрь 2009

3. Ю. И. Лобановский – Критерий возбуждения гидроакустических автоколебаний напорной системы, январь – февраль 2010

4. Ю. И. Лобановский – Гидроакустическая устойчивость гидроаккумулирующих станций, январь 2010

5. В. Л. Окулов, И. М. Пылев – Неустойчивость напорных систем. Доклады Академии наук, Энергетика, 1995, том 341, N 4.

6. В. Х. Арм, В. Л. Окулов, И. М. Пылев – Неустойчивость напорных систем гидроэнергоблоков. Известия Академии Наук, Энергетика, 1996.

7. V. L. Okulov, I. M. Pylev – The Behavior of Hydraulic Machinery under Steady Oscillatory Conditions. IAHR, 7-th International Meeting, 5 – 7 September 1995, Ljubljana, Slovenia.

8. Л. И. Седов – Механика сплошной среды, т. 2. Москва, Наука, 1976.

9. В. И. Брызгалов – Из опыта создания и освоения Красноярской и Саяно-Шушенской ГЭС. Производственное издание, 1998

10. Дж. В. Стретт (Лорд Рэлей) – Теория звука, т. II. Москва, Государственное издательство технико-теоретической литературы, 1955.

11. Г. С. Горелик – Колебания и волны: введение в акустику, радиофизику и оптику. Москва, Государственное издательство физико-математической литературы, 1959.

12. Н. В. Карлов, Н. А. Кириченко – Колебания, волны, структуры. Москва, Физматлит, 2001.

13. Ю. И. Лобановский – Отражает ли теория резонансного возбуждения автоколебаний напорных систем реальность? Март 2010

14. А. Л. Гуртовцев – Гидроаккумулирующие станции. Электрозавод, N 1, 2007

15. List of world’s tallest dams. Wikipedia

16. Ю. И. Лобановский – Первичный отбор ГЭС и ГАЭС с радиально-осевыми турбинами в группу риска по гидроакустической устойчивости, март 2010

17. Выявление причины аварии на ГЭС «Памир 1» продолжается. Сообщение для прессы. Pamir Energy, 2007

18. Важные события уходящего 2007 года по версии Asia-Plus. ASIA Plus, 2007

Юрий Лобановский,
кандидат физ.-мат. наук

04.04.2010
(«Гидротехническое строительство», № 7, 2010 год)

Продолжение темы

Б.Н. Юркевич. Отзыв на статью Ю.И. Лобановского «Автоколебания напорных систем и разрушение гидроагрегатов»

Ю.И. Лобановский. Анализ рецензии Б.Н. Юркевича на статью «Автоколебания напорных систем и разрушение гидроагрегатов»